The event horizon is an imaginary surface outside of a black hole within which nothing can escape. Somehow classic astrophysics says all the information from the original star that created the black hole and everything it’s eaten since is encoded on this imaginary surface.
In spacetime cells the surface is not imaginary. It is the cell on which all the mass-bearing and massless particles have collected, and its size is the same as the size of the event horizon.
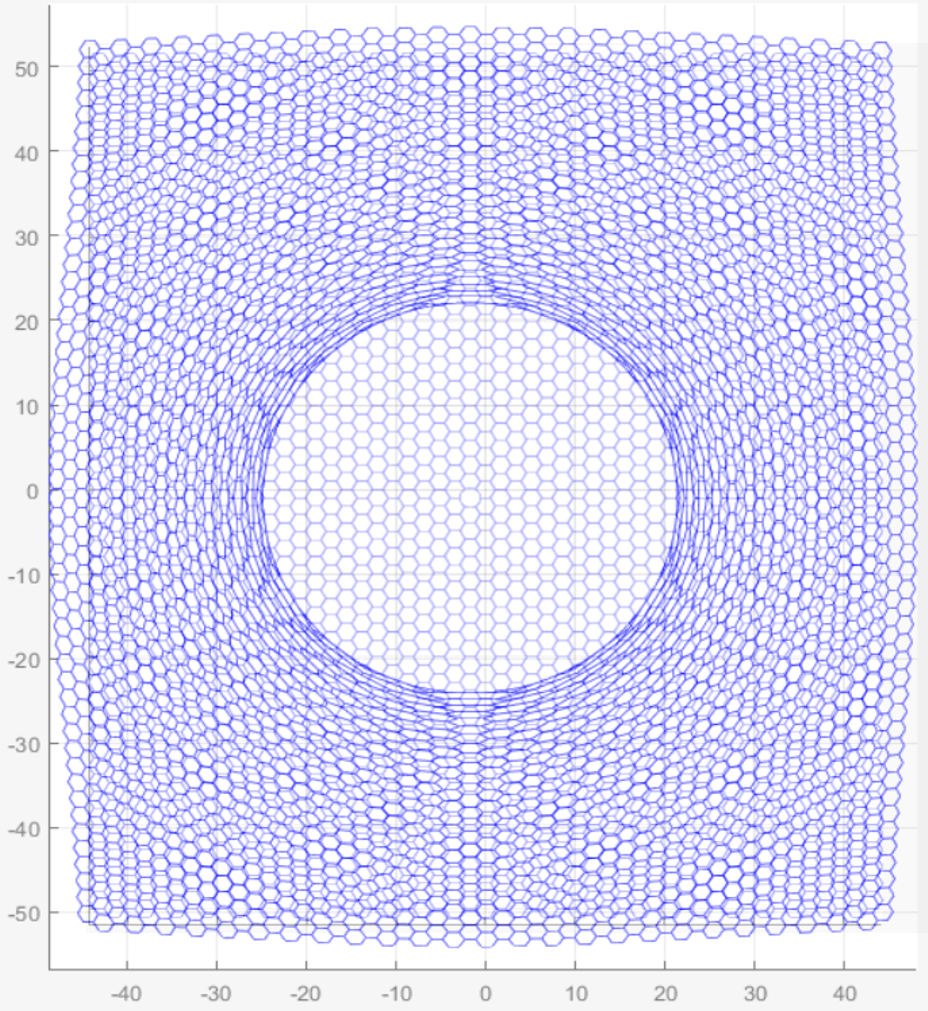
In the plot above, the top layer is the external view, where the heavily expanded cell is the black hole. The bottom layer is the internal view, where the small circular cell in the middle is the black hole. If you count the cells from the circular cell outward there are 13 cells. This is where the internal user would find the event horizon. Therefore, in the external view, the black hole cell has expanded to a radius of 13 cells, and in internal view the event horizon is at 13 cells.

Likely you’ve seen images of simulated black holes like the one above, where the area within the event horizon is completely black (except the accretion disk in front) and stars in the background near the horizon have extreme gravitational lensing. Black holes are useful to physics because of their extremes. Unsurprisingly, they are also helpful for the spacetime cells idea. The fact that the cell in actuality matches the size of the event horizon is profound and telling.
Up until now, I haven’t thought much about the dimensions of the external view. In the internal view, each cell has a diameter of 1 Planck length, regardless of how large it actually is in reality (that is in the external view). But what I’ve been referring to as “reality” does have a size and exists in a realm that has at least three spacial dimensions and one time dimension just like our universe (which exists within it). Is it possible to determine the actual dimension of the primordial cell, and would knowing that expose any deeper truths? Well since there’s nothing different between the primordial cell and a cell containing a black hole of the same energy content, and since the spacetime cell’s idea claims that the event horizon of a black hole is equivalent to the size of the cell the black hole occupies, if we knew the energy content of the universe, we could compute this.
At this physics site I found an estimate of the energy content of the universe as equivalent to 4.4•1052 kg. Of course this is an estimate (I found other values in the this ballpark), but the main thing is to compute the total amount energy scattered throughout our universe contained in all types of forms (e.g. bosons, regular matter, dark matter) except dark energy, which I believe is simply an artifact of the nature of spacetime cells. The equation for the radius of an event horizon, aka the Swarzschild Radius, is R = 2MG/c2. For the aforementioned energy estimate the radius of the primordial cell would be 6.89•109 light years.
What does this mean? Energy waves on the surface of the cell would travel at the speed of light. Presumably the membranes of cells can also grow at the speed of light. If this is the case, then the first cell division would have taken nearly 7 billion years. In the internal view, it only took one Planck time.
I’ve heard and read many accounts of the first second after the Big Bang. As Physics advances, it is able to predict closer and closer to time zero. Perhaps it’s because it doesn’t matter to physics, but General Relativity says time slows down when an object is close to a massive object relative to an observer away from the object. Mathematics breaks down at the point of a singularity, but predicts that time stops. What does it mean for time to stop? Does it actually stop or just get incredibly slow? 7 billion years of “real” external time for 10-43 seconds of internal time would seem like time stopping.